PONSTAT : Universitas Jember Virtual Statistics Laboratory
Pondok to Learn, Discuss, & Practice Statistics

Lecture Notes/ Handouts/ Tutorials

All graphics are produced using R in various packages

Lecture Notes

Sebagaimana telah disampaikan di halaman depan, bahwa kumpulan lecture notes/ handouts ini lebih menonjolkan pemaparan teori secara naratif yang dilengkapi dengan ilustrasi/ visualisasi menggunakan R. Topik-topik pada handout ini sangat luas mulai dari topik-topik pada statistika matematika, komputasi statistika dan aplikasi pada beberapa bidang. Jika anda memiliki catatan kuliah yang memanfaatkan R anda bisa berbagi catatan kuliah anda di halaman ini.

Ada beberapa ciri khas yang membedakan lecture notes di web ini diantaranya:

memuat uraian teori dengan menggunakan notasi matematika dengan format $\LaTeX$ sehingga notasi matematika ditampilkan sebagaimana mestinya, misalnya $E(X)=\int_{R_X} x f(x)\,dx$;
ilustrasi data dan analisis bersifat dinamik, pengguna dapat memilih data, memilih variabel, memilih model serta jenis luaran yang diinginkan, yang langsung direspon oleh server (sangat responsif);
pengguna bahkan dapat mengimpor datanya sendiri yang selanjutnya dianalisis sesuai keperluan;
selain luaran berupa numerik, hampir semua analisis dilengkapi dengan visualisasi grafik yang menambah makna analisis, dan mempermudah pemahaman. Untuk keperluan pemahaman, pemodelan statistika pada catatan kuliah ini disarankan menggunakan maksimum 2 variabel prediktor (bebas), untuk bisa memvisualisasikan grafiknya. Namun, di luar visualisasi grafik, jumlah variabel tidak dibatasi.

Anda dapat mengklik pada tombol Simak Handout pada tiap-tiap topik, atau anda bisa juga langsung memilih melalui dropp down menu di samping.

Cek Daftar Handout Yang Lain

Topik Statistika Matematika

		Kepadatan Distribusi Diskrit Dalam topik ini dibahas beberapa distribusi diskrit (Binomial, Negatif Binomial, Geometri, Poisson), mulai bentuk kepadatannya, selanjutnya pembaca dapat bereksplorasi memeriksa grafik fungsi peluang, membangkitkan data dan memeriksa histogram dari data yang dibangkitkan dan sebagainya Simak Handout
		Kepadatan Distribusi Kontinu Dalam naskah ini dibahas beberapa distribusi kontinu (Normal, Gamma, Uniform) mulai bentuk fungsi kepadatannya, selanjutnya pembaca dapat bereksplorasi memeriksa grafik fungsi peluang, membangkitkan data dan memeriksa histogram dari data yang dibangkitkan.Simak Handout
		Bangkitan Data Distribusi Keluarga Eksponensial Dalam topik ini dibahas membangkitkan data dari beberapa distribusi keluarga eksponensial (Normal, Gamma, Poisson, Binomial), selanjutnya memeriksa histogram, Normal-plot, serta menguji normalitas datanya dengan beberapa uji yang ada. Simak Handout
		Sebaran Samplel Acak Dalam topik ini dibahas Sifat-sifat sampel acak seperti sebaran rata-rata sampel, mean dan variansnya. Diilustrasikan juga ide Teorama limit pusat, yang menyatakan bahwa apapun sebaran data awalnya, jika ukuran sampelnya besar, sebaran skor bakunya akan mendekati sebaran Gaussian baku $Z~N(0,1)$ Simak Handout
		Penduga Likelihood Maksimum & Kuadrat Terkecil Dalam topik ini dibahas Ide fungsi likelihood dan maksimumnya yang menghasilkan penduga likelihood maksimum. Posisi maksimum dari fungsi likelihood diilustrasikan dengan menggambar kontur dan perspektif dari fungsi likelihood. Demikian juga, untuk fungsi Bentuk Kuadrat (Quadratic Form) posisi nilai minimumnya juga diilustrasikan dengan grafik kontur dan perspektif. Simak Handout

Topik Model Statistika Linear

		Presentasi Grafik dengan `graphics, ggplot2` Grafik adalah salah satu kekuatan atau keunggulan yang dimiliki R. Dalam topik ini dibahas pembuatan grafik dengan menggunakan dua paket yaitu `graphics` dan `ggplot2`, mulai dari mendesain lay-out dan memmuat beberapajenis grafik baik univariat (histogram, box-plot, qq-plot) dan bivariate (diagram pencar). Simak Manual
		Aljabar Matriks Dalam topik ini dibahas aljabar matriks yang terkait dengan statistika Simak Handout
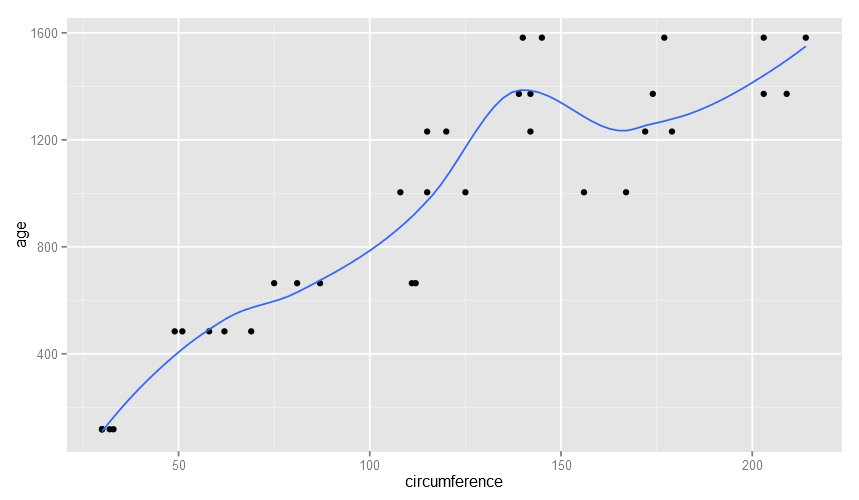
		Regresi Sederhana Dalam topik ini dibahas uji regresi linier sederhana, mulai pemeriksaan asumsi secara grafik maupun melalui uji normalitas. Selanjutnya melakukan uji regresi dan memeriksa (i) signifikansi koefisien regresi, (ii) Nilai R-square, dan AIC untuk memilih model yang lebih baik. Anda dapat mencermati dampak pelanggaran asumsi terhadap nilai goodness of fit (GOF) Simak Handout
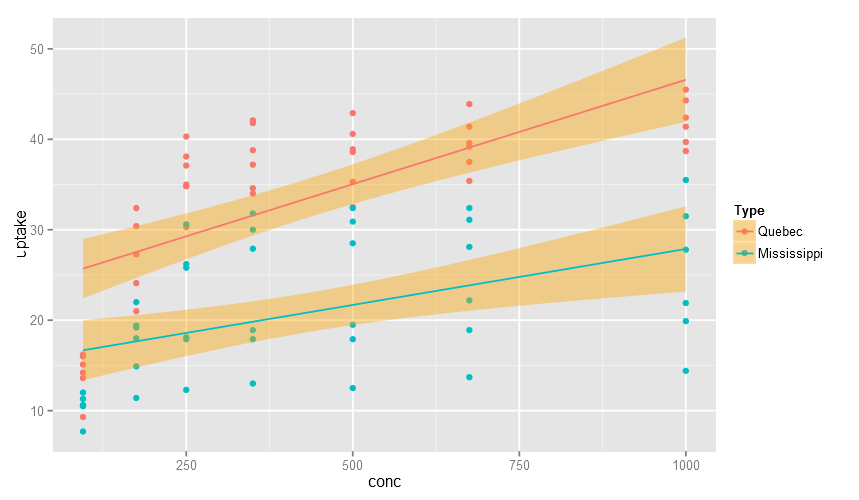
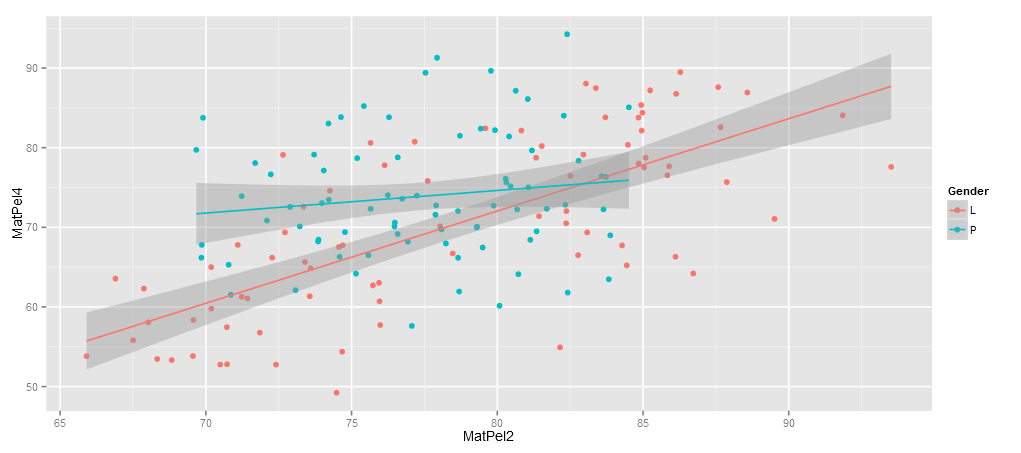
		Regresi Dengan Kelompok Dalam topik ini dibahas uji regresi linier dengan peubah kualitatif/kelompok/grup, baik grup real, ataupun grup laten yang dihasilkan oleh pengklasteran. Kegiatan dimulai dengan pemeriksaan asumsi secara grafik maupun melalui uji normalitas, selanjutnya melakukan uji regresi dan memeriksa (i) signifikansi koefisien regresi, (ii) Nilai R-square, dan AIC untuk memilih model yang lebih baik. Anda dapat mencermati dampak pertimbangan variabel kelompok terhadap nilai goodness of fit (GOF) Simak Handout

Topik Model Statistika Lanjut dan NonLinier

	GLM (Model Linier Tergereralisir) Dalam topik ini dibahas uji regresi yang memiliki prediktor linier peubah kualitatif/kelompok/grup, baik grup real, ataupun grup laten yang dihasilkan oleh pengklasteran dan berbagai skala respon (seperti kontinu, diskrit, biner). Hubungan prediktor linier dengan respon dihubungkan oleh fungsi kontinu dan differensiabel (fungsi link. Kegiatan dimulai memeriksa (i) signifikansi koefisien regresi, (ii) Nilai Devians, dan AIC untuk memilih model yang lebih baik. Juga disajikan grafik untuk eksplorasi hubunagn variabel dan diagnostik normalitas data seperti, Boxplot, QQ-Norm, dan Diagram Pencar. Anda dapat mencermati dampak pertimbangan variabel kelompok terhadap nilai goodness of fit (GOF) Simak Handout
	GEE (Model untuk Regresi data Longitudinal) Dalam topik ini dibahas uji regresi dengan respon yang diukur secara berulang atau terklaster. Kegiatan dimulai dengan eksplorasi data (termasuk menghitung korelasi), selanjutnya melakukan pengepasan regresi untuk berbagai sebaran dan tipe korelasi. Simak Handout
	Logit Ordinal (Model untuk respon Ordinal ) Dalam topik ini dibahas uji regresi dengan respon bersekala ordinal dengan kategori lebih dari 2 (dua). Kegiatan dimulai dengan eksplorasi data (termasuk menghitung korelasi), selanjutnya melakukan pengepasan regresi untuk berbagai sebaran dan tipe korelasi. Simak Handout
	Model untuk respon Longitudinal dengn sekala Ordinal ) Dalam topik ini dibahas uji regresi dengan respon longitudinal bersekala ordinal dengan kategori lebih dari 2 (dua). Kegiatan dimulai dengan eksplorasi data (termasuk menghitung korelasi), selanjutnya melakukan pengepasan regresi untuk berbagai sebaran dan tipe korelasi. Simak Handout
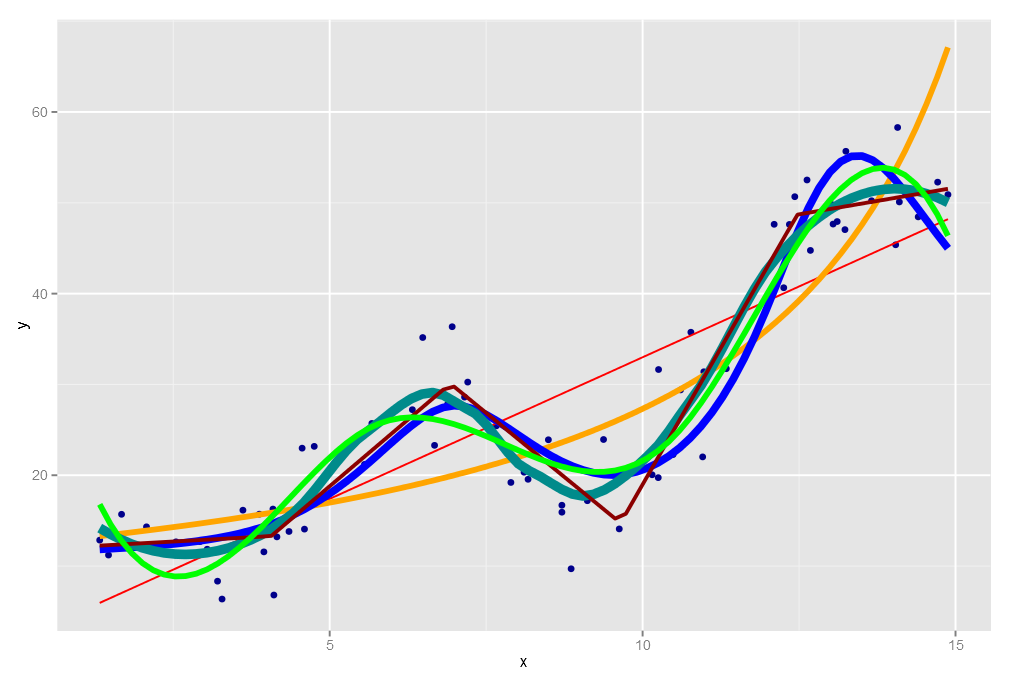
	*Konsep Penghalus (Smoother)* Dalam topik ini dibahas regresi nonlinier dan konsep serta visualisasi penghalus (berbagai penghalus spline) dan penghalus regresi lokal (loess), sebagai pengantar *GAM (Generalised Additive Model)* Simak Handout

Topik Komputasi Statistika dan Lain-lain

		*Simulasi MC (Acceptance Rejection* )** Dalam topik ini dibahas cara membangkitkan data dari peubah acak yang hanya diketahui fungsi kepadatannya, sementara bentuk fungsi kumulatif (apalagi inversnya), tidak terlacak (tidak mudah diturunkan). Cara simulasi ini termasuk kelompok Simulasi Monte Carlo. Simak Handout
		Estimasi Densitas Dalam topik ini, pengguna dapat mempelajari konsep estimasi densitas serta melakukan perhitungan estimasi dengan berbagai metode, serta menghitung secara sederhana besarnya bandwidth optimal Simak Handout
		Validasi Klaster Ada banyak cara untuk membuat klaster (melakukan analsis klaster), baik dilihat dari prosedur perhitungan maupun dari jarak yang digunakan. Lebih sering tiap metode menghasilkan klaster yang berbeda. Dalam topik ini dibahas salah satu metode untuk melakukan vaidasi klaster, sehingga pegguna dapat memilih cara yang lebih sesuai kondisi data dan tujuan pengklasteran. Selanjutnya kita dapat melakukan analisis klaster lebih detail menggunakan salah satu metode yang direkomendsikan Simak Handout
		Aplikasi Keragaman Hayati Biodiversity Analisis keragaman hayati ( Biodiversity) selain memanfaatkan metode statistika secara umum (seperti berrbagai analisis multi variat), juga membutuhkan statistika khusus yang hanya diperlukan dikalangan para biometrisi (biometrikawan). Salah satunya adalah menghitung dan membuat grafik kelimpahan spesies (species richness) dan menghitung berbagai jarak ekologi. Simak Handout
		Analisis Item Respon Theory Analisis IRT ( Item Response Theory) merupakan metode modern untuk menganalisis kualitas butir soal yang menggunakan pendekatan model logistik. Dalam tutorial ini anda bisa berlatih menerapkan IRT untuk menganalisis butir soal tipe dikotomus menggunakan model 1 PL (model Rasch,untuk menganalisis tingkat kesulitan butir soal), model 2 PL (untuk menganalisis tingkat kesulitan dan diskriminasi butir soal) dan 3 PL (untuk menganalisis tingkat kesulitan, tingkat diskriminasi dan tebakan butir soal). Simak Handout

PONSTAT : Universitas Jember Virtual Statistics Laboratory
Pondok to Learn, Discuss, & Practice Statistics

Lecture Notes/ Handouts/ Tutorials